Factors and Prime Factors
Understanding Number Properties is really important for solving many different types of problems. Number Properties are all about how numbers behave and interact with each other in different situations. Knowing and practicing these properties can be super helpful in your classes, exams, and even everyday life. When you understand Number Properties, you can predict how numbers will behave and what outcomes to expect in your problems.
This post will focus on a specific aspect of Number Properties called factors and prime factors. If you are feeling comfortable with factors and prime factors and are ready to jump to our other posts in this series, click the the links below:
Before we dive too deep into these concepts, let's define a few important terms:
Integer: An integer is a whole number and their opposites, like 3 or -3. An integer can be positive or negative, but numbers like -3.5 or 3.5 are not integers.
Dividend: In division, the number you want to divide is called the dividend. For example, in the problem 24 ÷ 8, 24 is the dividend.
Divisor: In division, the number you divide by is called the divisor. So in the problem 24 ÷ 8, 8 is the divisor.
Evenly Divisible: A number is evenly divisible when you can divide it by another number and get a whole number as a result (quotient) without any remainder. For instance, 24 is evenly divisible by 8 because when you divide 24 by 8, you get the whole number 3 as the quotient.
Prime Number: A number is prime when it can only be divided evenly by itself and 1. The smallest prime number is the number 2 because it can only be divided by itself and 1. The number 1 is not considered prime.
Now, let's explore Factors and Prime Factors.
Factors
A factor is a special type of divisor. When you divide a dividend by a factor, the result is an integer, and the division is evenly divisible. For example, when you divide 24 by 8, you get 3 as the quotient, making 8 a factor of 24.
Finding factors can be done using a factor table. In a factor table, you find factor pairs, two numbers that, when multiplied, give you the original number you're factoring.
For example, the factor table for 24 shows that it has 8 factors: 1, 2, 3, 4, 6, 8, 12, and 24.
When creating a factor table, it is important to pay close attention to details, as it can be easy to miss a pair. To make sure you include all factors, you need to know your math facts and divisibility rules.
Factor table for the number 24
Factors can be found by finding factor pairs whose products will result in 24. (i.e. 1*24 = 24)
Prime Factors
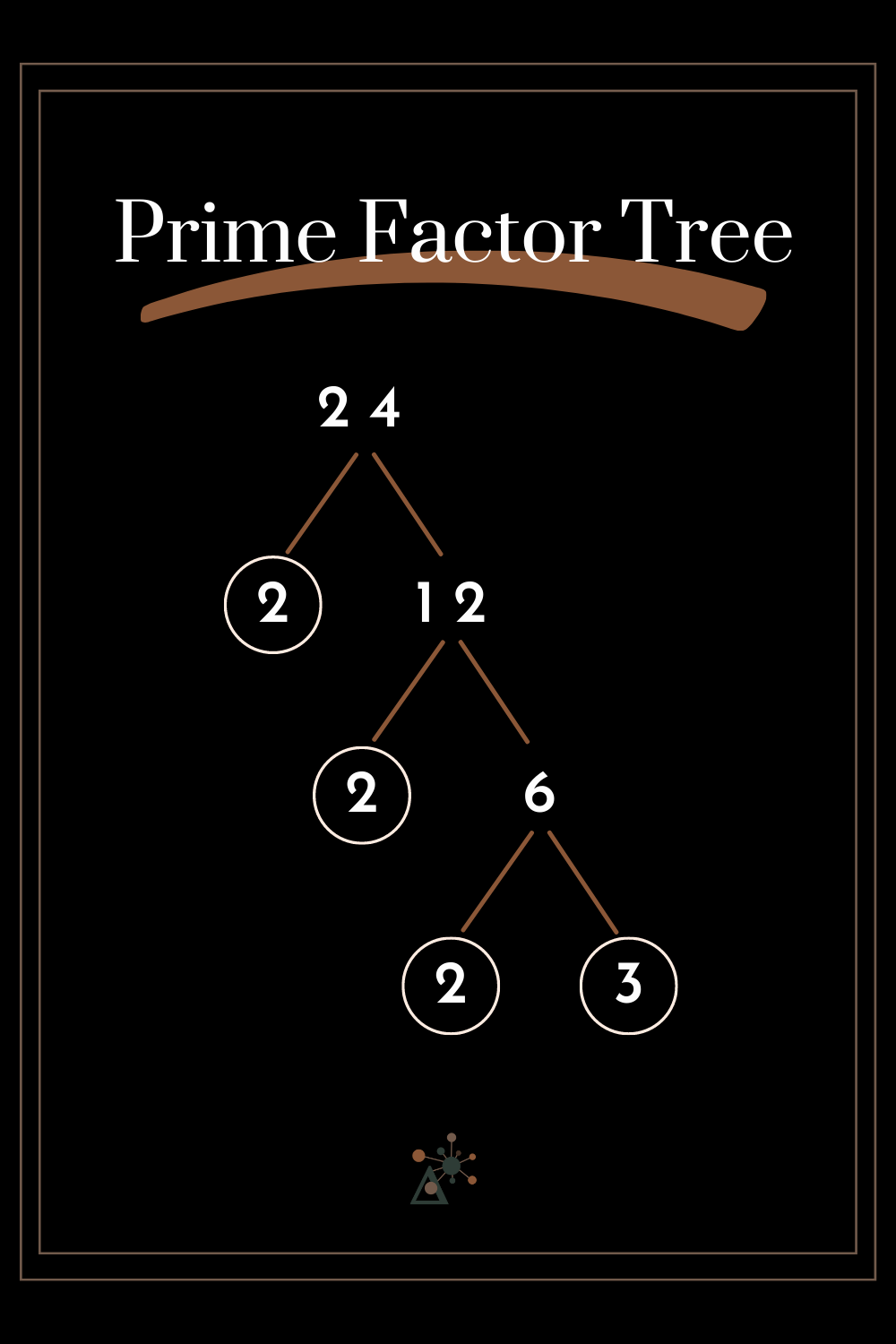
Another way to account for all factors is by understanding prime factors. Prime factors are the building blocks of a number, and all factors of a number are some combination of its prime factors. You can find prime factors by creating a prime factor tree. For instance, the prime factors of 24 are 2 * 2 * 2 * 3, and when you multiply them together, you get 24.
Prime Factor Tree for the number 24
Using a factor pair, factor until only prime numbers remain. All the prime factors in the example are circled.
Prime Factors Advanced
Prime factors also help you determine the total number of factors a number has. By using a little trick, you can find this out without knowing all the factors. Let's break it down:
Write the prime factors of a number using exponents (even if the exponent is 1).
Add 1 to each exponent.
Multiply the sums from Step 2.
The result will give you the number of factors the number has!
Conclusion
Knowing factors is helpful in various situations, such as finding the greatest common factor (GCF) to simplify fractions, dividing quantities into equal pieces, exchanging money, and even factoring polynomials.
So, keep exploring Number Properties, and remember to have fun with math!