Evaluating Functions - When Input Is an Expression
In our previous post, we explored different methods for evaluating functions—algebraically, graphically, and through tables—specifically, when the input is a rational number. If you need a refresher, you can find the post here.
In that lesson, we focused on finding the corresponding y-value (output) for a given x-value (input). However, there are instances when the input is an expression rather than a simple rational number, resulting in an output that is also an expression.
Note: While we commonly use x and y as variables, any letters can represent the input and output. In function notation, the variable inside the parentheses is the input, and the entire notation is the output. For instance, in the function p(n), n is the input, and p(n) is the output.
How to Evaluate Functions When the Input Is an Expression
1. Substitute the expression wherever the variable appears, keeping the expression in parentheses.
2. Utilize the order of operations to expand the function as necessary.
3. Simplify the expression by combining any like terms.
Let’s take a look at a few examples:
Example A
The text reads, “Evaluate the following function.” Underneath it reads “A. Given f(x)=4x+5, find f(x+2).” Below, the problem is solved. “x+2” replaces “x.” Problem now reads “=4(x+2)+5”, then “4x+8+5”, then 4x+13. Finally, in a shaded box, the answer says “f(x+2)=4x+13.
Example B
The text reads, “Evaluate the following function.” Underneath it reads “B. Given g(h)=-h^2+3h+1, find f(h^2).” Below, the problem is solved. “h^2” replaces “x.” Problem now reads “=-(h^2)^2+3(h^2)+1”, then “-h^4+3h^2+1”. Finally, in a shaded box, the answer says “f(h^2)=-h^4+3h^2+1.
Example C
The text reads, “Evaluate the following function.” Underneath it reads “C. Given f(t)=5t-7, find f(3t).” Below, the problem is solved. “3t” replaces “t.” Problem now reads “=5(3t)-7”, then “15t-7”. Finally, in a shaded box, the answer says “f(3t)=15t-7”.
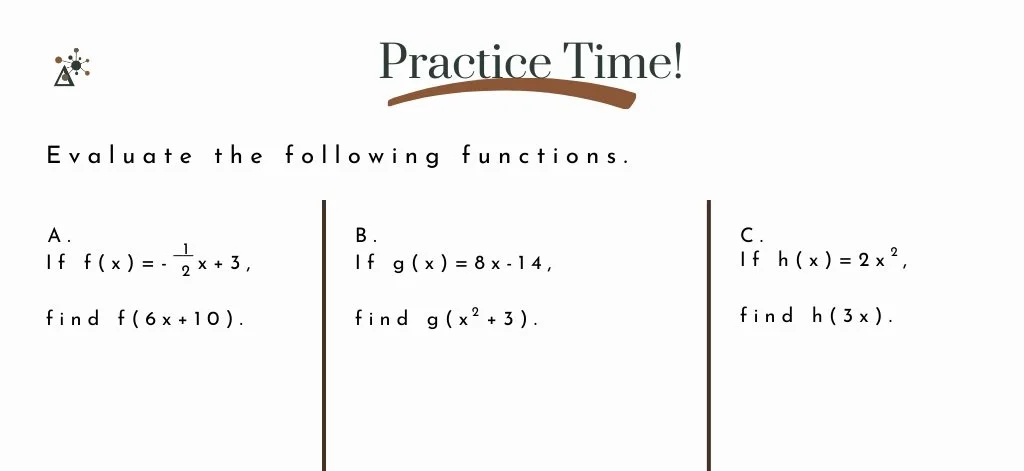
Practice Time!
Evaluate the following functions. The answers can be found at the end of this post.
Conclusion
Whether the input variable is a number or an expression, the process of evaluating a function involves replacing all variables with the given values and simplifying as much as possible. This may result in a constant or an expression.
Answers to Practice Time!
-
= -3x - 3
-
= 8x^2 + 10
-
= 18x^2